Birleşme, bir küme üzerine tanımlanmış ikili işlemlerin ayırt edici özelliklerinden biridir. Bu özelliği sağlayan ikili işlemlere birleşmeli işlem denir. Açık olarak bu özellik, (xy)z = x(yz) demektedir, yani üç elemanı "çarparken" işlem sırasının önemli olmadığını söylemektedir, bir başka deyişle birleşme özelliği işlem yaparken paranteze gerek olmadığını söylemektedir. Örneğin tamsayılar kümesi Z üzerine tanımlanmış olan toplama işlemi birleşmeli bir işlemdir ancak çıkarma işlemi birleşmeli değildir, çünkü (x + y) + z = x + (y + z) eşitliği her 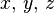 için sağlanmasına karşın, (x − y) − z = x − (y − z) eşitliği
için sağlanmasına karşın, (x − y) − z = x − (y − z) eşitliği  için sağlanmaz.
için sağlanmaz.
Üç 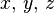 elemanı için geçerli olan bu özellik elbet n tane eleman için de geçerlidir. Örneğin (xy)(zt) = ((xy)z)t = (x(yz))t = x(y(zt)).
elemanı için geçerli olan bu özellik elbet n tane eleman için de geçerlidir. Örneğin (xy)(zt) = ((xy)z)t = (x(yz))t = x(y(zt)).
 , X kümesi üzerine bir ikili işlem ise ve her
, X kümesi üzerine bir ikili işlem ise ve her  için
için  ise,
ise,  ikili işleminin birleşmeli işlemolduğu söylenir. Toplama, çarpma gibi cebirde rastlanan işlemlerin birçoğu birleşme özelliğini sağlar. Ancak çıkarma işlemi (tamsayılar kümesi üzerinde) birleşmeli işlem değildir çünkü x − (y − z) sayısı eğer z, 0'a eşit değilse (x − y) − z'ye eşit değildir.
ikili işleminin birleşmeli işlemolduğu söylenir. Toplama, çarpma gibi cebirde rastlanan işlemlerin birçoğu birleşme özelliğini sağlar. Ancak çıkarma işlemi (tamsayılar kümesi üzerinde) birleşmeli işlem değildir çünkü x − (y − z) sayısı eğer z, 0'a eşit değilse (x − y) − z'ye eşit değildir.
Birleşme özelliği sağlayan yapılarda işlemler yapılırken parantez gerekmez. Bu yüzden  ve
ve  yerine,
yerine,  yazılır. Aynı şey dört eleman çarpılırken de geçerlidir: Birleşme özelliğini sağlayan bir işlem sözkonusu olduğunda,
yazılır. Aynı şey dört eleman çarpılırken de geçerlidir: Birleşme özelliğini sağlayan bir işlem sözkonusu olduğunda,  ,
,  ,
,  , gibi çarpımlar parantezsiz olarak
, gibi çarpımlar parantezsiz olarak  olarak yazılır.
olarak yazılır.
Birleşme özelliğini sağlamayan yapılarda x3 elemanını tanımlamak bile sorun olabilir, nitekim bu eleman  olarak tanımlanabileceği gibi
olarak tanımlanabileceği gibi  olarak da tanımlanabilir. x4 için çok daha fazla seçenek olabilir.
olarak da tanımlanabilir. x4 için çok daha fazla seçenek olabilir.
Matematiğin en önemli işlemlerinden biri fonksiyonların bileşme işlemidir. Eğer X bir kümeyse, Fonk(X, X), X kümesinden X kümesine giden fonksiyonlar kümesi olsun. Eğer  Fonk(X, X) ise, gene X kümesinden X kümesine giden ve adına "f ile g fonksiyonlarının bileşkesi" denilen f o g fonksiyonunu şöyle tanımlayalım: Her
Fonk(X, X) ise, gene X kümesinden X kümesine giden ve adına "f ile g fonksiyonlarının bileşkesi" denilen f o g fonksiyonunu şöyle tanımlayalım: Her  için, (f o g)(x) = f(g(x)) olsun. Bu, Fonk(X, X) kümesi üzerine bir işlemdir. Bu işlemin birleşme özelliği vardır.
için, (f o g)(x) = f(g(x)) olsun. Bu, Fonk(X, X) kümesi üzerine bir işlemdir. Bu işlemin birleşme özelliği vardır.
Cebirde ender olsa da birleşme özelliğini sağlamayan işlemler önemli olabilir. Örneğin Lie cebirlerindeki köşeli parantez işlemi birleşmeli değildir. Öte yandan Lie cebirlerinde köşeli parantez işlemi, Jacobi eşitliği sayesinde, birazcık olsun birleşme özelliğini sağlar.
Kümelerde Birleşim İşareti [değiştir]
kümelerde birleşme işareti "U" şekilindedir.İki ya da daha çok kümenin elemanlarını bir araya getirme işlemidir. A ve B iki küme ise bu iki kümenin birleşimi A U B şeklinde gösterilir
örneğin: A = { 1, 3, 5, 7 }, B = { 3, a, b } ise A U B kümesini şema ile gösterip tarayalım.

 .
.
S deki * ikili işlemi, birleşme yasasına uymuyorsa buna birleşmesiz (İngilizcesi non-associative) diyoruz. Sembolik olarak,
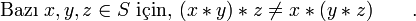
Değerlendirme sırası işlemi için sorun değildir. Örneğin:

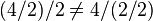

Sonlu toplamanın genellikle ilişkili olmadığına dikkat edin. Örneğin:

Benzer şekilde
